Heat loss from pipes is a major concern in systems that involve fluid transport. To maintain process fluids at desired temperatures, protect the system against freezing, reduce energy costs, and ensure efficient operation, it is crucial to understand the factors that contribute to heat loss and implement effective solutions.

This comprehensive guide offers a complete understanding of heat loss from pipes, including the factors that affect it and how to calculate it.
Types of Heat Loss from Pipes
Heat loss from pipes occurs when the fluid that they transport has a higher temperature than the surrounding environment. This transfer of heat can occur through one or a combination of three modes of heat transfer: conduction, convection, and radiation.
Conductive Heat Loss
Elevate Your Engineering With Excel
Advance in Excel with engineering-focused training that equips you with the skills to streamline projects and accelerate your career.
Conductive heat loss happens when heat passes through the walls of the pipe and the insulating materials surrounding it. The amount of conductive heat loss is influenced by factors such as the thermal conductivities of the materials, their thickness, and the temperature difference between the inner and outer surfaces of the pipe.
The formula for conductive heat transfer is:
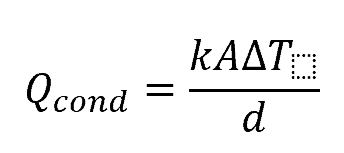
Where:
- Qcond = amount of heat lost through conduction [W]
- k = thermal conductivity of the pipe or insulating material [W/m-K]
- A = surface area of the material [m2]
- ΔT = temperature difference across the pipe material [K]
- d = thickness of the material [m]
Thermal conductivity is a constant specific to the physical properties of a given material that measures its ability to transfer heat. Some common values, as measured at room temperature, of materials are 45 W/m-K for steel and 398 W/m-K for copper.
Conductive heat loss can be reduced by using materials with low thermal conductivity, increasing the thickness of the pipe wall, and using appropriate insulation.
Convective Heat Loss
Convective heat loss in pipes occurs when heat is transferred from the pipe surface to the surrounding fluid (usually air or water) by means of convection. This type of heat transfer occurs when the fluid flows over the surface of the pipe, carrying away the heat from the surface. The rate of convective heat transfer depends on the fluid velocity, temperature, density, and viscosity, as well as the geometry and orientation of the pipe.
The formula for convective heat transfer is:
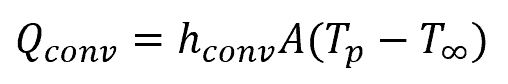
Where:
- Qconv = amount of heat lost through convection [W]
- hconv = convective heat transfer coefficient [W/m2-K]
- Tp = temperature of the pipe surface [K]
- T∞ = temperature of the surrounding environment [K]
Note that this equation is an oversimplification of the process of convection. In reality, the convective heat transfer coefficient is not constant and is dependent on the temperature difference and the nature of fluid flow over the surface of the pipe. Especially if the temperature difference is large, more complex equations or empirical correlations may be needed to accurately predict the convective heat transfer rate.
Generally, the effect of convection can result from a combination of forced and free convection. To calculate the convective heat transfer coefficient for each of these components, the Nusselt numbers can be obtained using the Churchill and Bernstein, and Churchill and Chu correlations. Once the Nusselt numbers are found, the total convective heat transfer coefficient can be calculated using the formula:
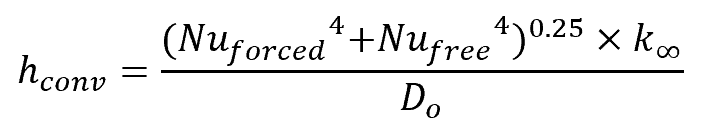
Where:
- Nuforced = Nusselt number for the forced convection component [unitless]
- Nufree = Nusselt number for the free convection component [unitless]
- k∞ = thermal conductivity of the surrounding environment [W/m-K]
- Do = outside diameter of the pipe [m]
Convective heat loss can be minimized by increasing the insulation thickness around the pipe, or by reducing the fluid flow velocity over the pipe surface.
Radiative Heat Loss
Radiative heat loss occurs when heat is emitted from the surface of the pipe as electromagnetic radiation. The rate of radiative heat loss depends on the surface temperature of the pipe and its emissivity.
Remember that the formula for radiative heat transfer is:
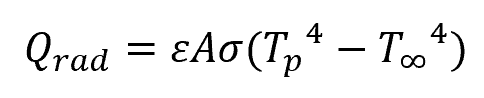
Where:
- Qrad = amount of heat lost through radiation [W]
- ε = surface emissivity of the pipe material [unitless]
- σ = Stefan-Boltzmann constant (5.669 × 10−8 W/m2-K4)
Note that surface emissivity is a dimensionless quantity that represents the efficiency of a surface in emitting thermal radiation compared to a perfect blackbody emitter. Its value is mainly dependent on the material composition and ranges from 0 to 1, where 0 represents a surface that does not emit any radiation, and 1 represents a surface that emits radiation as a perfect blackbody emitter.
Radiative heat loss can be reduced by using materials with low emissivity or by applying a reflective coating to the pipe’s surface.
Piping Heat Loss Calculation
To account for all modes of heat transfer in heat loss analysis, components contributing to heat loss are typically represented in terms of thermal resistances— a measure of an object’s ability to resist heat transfer.
The formula for the conductive thermal resistance of a pipe is:
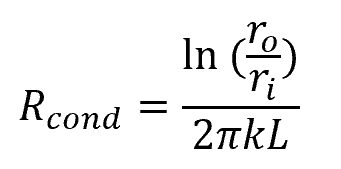
Where:
- Rcond = conductive thermal resistance [K/W]
- ro = outer radius of the pipe [m]
- ri = inner radius of the pipe [m]
- L = pipe length [m]
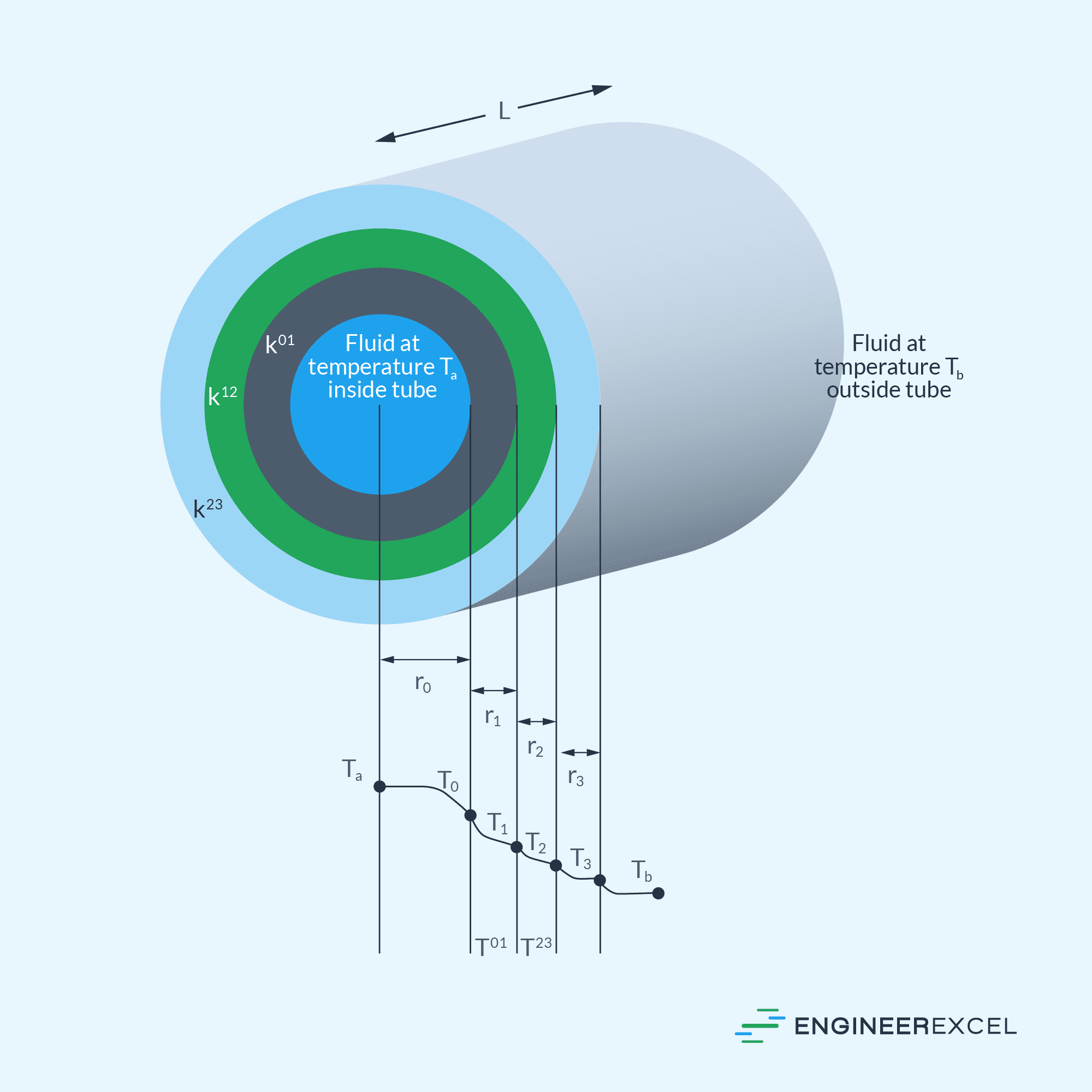
For pipes with multiple layers of insulation materials used, each material’s conductive thermal resistance is calculated separately, then summed into the overall system resistance.
On the other hand, the formula for the convective thermal resistance is:
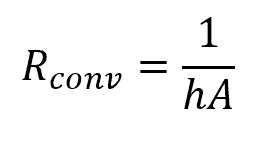
Where:
- Rconv = convective thermal resistance [K/W]
Lastly, the formula for the radiative thermal resistance becomes:
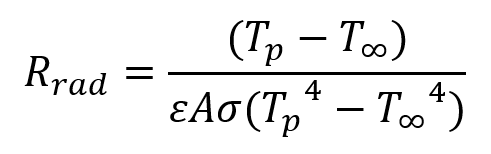
Where:
- Rrad = radiative thermal resistance [K/W]
These thermal resistances can be combined in series, such as the diagram shown below, to calculate for the total heat loss from pipes. The total thermal resistance then becomes:
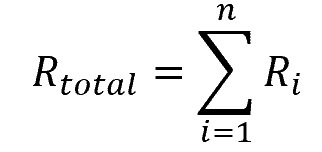
Where:
- Rtotal = total thermal resistance against heat loss [K/W]
- n = number of heat loss components
Note that the overall heat transfer coefficient can be obtained from the total thermal resistance using the formula:
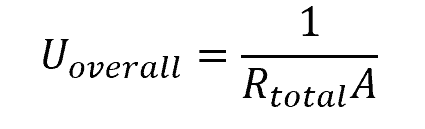
Where:
- Uoverall = overall heat transfer coefficient of the piping system [W/m2-K]
Consequently, both the total thermal resistance and the overall heat transfer coefficient can be used to calculate for the total heat loss using the formulas:
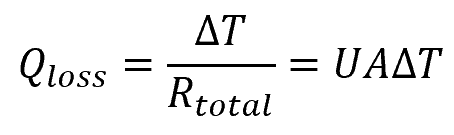
Where:
- Qloss = total heat loss of a piping system [W]
- ΔT = temperature difference between the fluid and the surrounding environment [K]
In practical low-to-medium temperature applications, convection and radiation typically contribute only 10% to the overall heat loss of a system. Especially for radiation, the outermost surface must be well above ambient temperature for significant heat loss to happen. As a result, some designers choose to simplify their calculations by only considering conduction and adding 10% to account for convective and radiative heat loss.
Lastly, it is important to note that piping heat loss is usually calculated per linear distance rather than the entire area of the pipe. This is because expressing the heat loss per unit length of pipe allows for easier comparison of different pipe lengths and configurations. It also simplifies the design process since it is easier to calculate and compare the heat loss per unit length of pipe rather than the total heat loss of the entire system.
