The Hazen-Williams Equation is used to calculate the head loss (pressure loss) of water due to its flow through a straight pipe. It does not consider other sources of head loss, such as elevation change, direction change, or pipe restrictions.
The equation is dependent on the interior pipe diameter, the velocity of the fluid moving through, and the Hazen-Williams coefficient, which describes the roughness of the interior pipe surface and can be found in a look-up table.
What is the Hazen-Williams Equation?
The Hazen-Williams Equation can be written in several ways, depending on what variable is being solved for.

Flow Rate Form

Elevate Your Engineering With Excel
Advance in Excel with engineering-focused training that equips you with the skills to streamline projects and accelerate your career.
Using standard nomenclature and SI units, the Hazen-Williams Equation takes the form below:
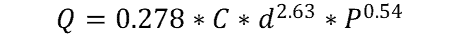
Where:
- Q = fluid flow rate (m3/s)
- d = pipe internal diameter (m)
- C = Hazen-Williams Coefficient, an empirically derived number that describes the interior pipe surface roughness
- P = Head loss per length of pipe (Pa/m)
This form of the equation solves for the output velocity of the fluid in the pipe, given the losses.
Head Loss Form
The equation above can be rearranged to solve for the head loss over the length of pipe.

Where
- P = head loss per one meter length of the pipe (Pa/m)
This further simplifies to:

To use the equation in this form, the output, P, gives the pressure loss per length of pipe. You would then need to multiply P by the length of pipe, in meters, to get the overall head loss for the given pipe section.
Head Loss Form (US Customary Units)
Using standard nomenclature and US customary units, the unit-specific Hazen-Williams Equation follows the form below:
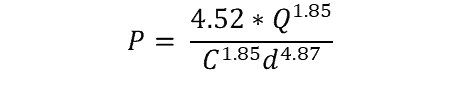
Where:
- P = head loss per one foot length of the pipe (psi/ft)
- Q = flow rate (gpm)
Hazen-Williams Equation Calculator
Hazen-Williams Coefficients
Hazen-Williams Coefficients are based on experimental measurements taken by Hazen and Williams in 1902. The pair was able to publish their work with a list of coefficients that were empirically derived, and the work became fundamental to the design of pipe systems, especially in the fields of civil engineering and mechanical building systems. Engineers and designers use the equation to determine head loss in systems such as irrigation, residential water supply, and building fire suppression.

Some common Hazen-Williams Coefficients are summarized in the table below.
Hazen-Williams Equation Example
Consider the example problem below:
Problem
City planning engineers must estimate the maximum head loss of the fresh water delivery pipe that is being installed to a new high rise. The pipe will tap into the main water line approximately 300m from where it enters the building, and is made of brass with an internal diameter of 0.28m and a flow rate of no more than 6.3*10-2 m3/s.

Solution
Use the head loss form of the Hazen-Williams Equation to solve for head loss per meter.

From the problem statement, the maximum flow rate, Q, is 6.3*10-5 m3/s and the pipe diameter, d, is 0.28m. The pipe material is given as brass, so from the table of Hazen-Williams coefficients, C, is equal to 130. Plugging them in to the above equations yields:
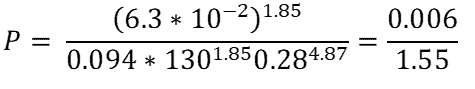
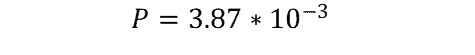
P is given in pascals per meter of pipe, so the solution above must be multiplied by the length of pipe (l) to obtain the overall head loss.
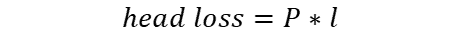
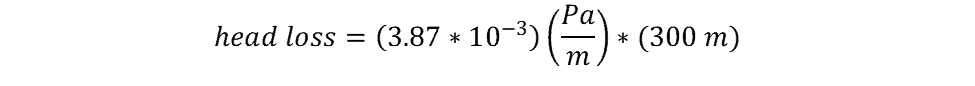
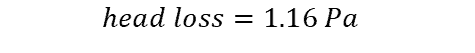
In this example, the maximum total head loss over the 300m length of pipe is 1.16Pa.
Hazen-Williams Equation vs. Darcy-Weisbach Equation
The main benefit of the Hazen-Williams Equation is that the coefficient, C, is unrelated to the Reynolds number, greatly simplifying the calculation. The alternative to this method is to use the Darcy-Weisbach Equation, which includes a friction factor analogous to the Hazen-Williams Coefficient, but one that is dependent on the Reynolds number.
Finding the friction coefficient in the Darcy-Weisbach Equation a multi-step process. The first step is to calculate the Reynolds number for the fluid in question. Then, the relative roughness must be determined; this is usually accomplished from published lists for given materials. Finally, the friction factor can be determined using the Moody diagram.
By separating the coefficient from the Reynolds number, Hazen and Williams were able to greatly simplify the equation and speed up the calculation. This gives the Hazen-Williams equation great utility, but it cannot be applied in every situation.
When to Use the Hazen-Williams Equation
The Hazen-Williams Equation is limited in its use, and does not apply to all fluid flow situations. If used incorrectly, the results will not accurately model the real-life situation. Therefore, it is important to know the following rules for use:
The Hazen-Williams Equation only applies to water, or liquids with a similar viscosity to water (a viscosity of approximately 1.12 x 10-6 m2/s, or 1.22 x 10-5 ft2/s).

The Hazen Williams Equation is only applicable within a well-defined temperature range. Because the equation is based on experimental data, results are only valid within the temperature range that the original data was taken, or from 40°F to 75°F (4°C to 24°C). Outside of this range, the fluid viscosity is no longer applicable, and the results of the Hazen-Williams Equation are invalid.
Only pressurized pipe flow can use this equation, i.e. the pipe must be completely full of water, with no other fluids (like air) inside. The equation assumes that the entire interior surface of the pipe is in contact with the fluid. Therefore, it does not apply to open channel flow.
The equation does not apply if the pressure is too high, above roughly 175psi. For higher pressures, refer to the Darcy-Weisbach Equation.
