The drag induced on an object moving through the air is an important value in aerodynamic calculations. For example, an airplane will need to have enough thrust to overcome the induced drag to either accelerate or maintain its speed. To determine the drag induced on a body, the drag equation is used.
Understanding Drag
Aerodynamic drag is an important concept when calculating the necessary parameters for objects, such as aircraft or rockets, as they move through the air. Specifically, in addition to gravity, aerodynamic drag imparts a force upon an object. This force must be overcome by the propulsion system to accelerate the body through the air.
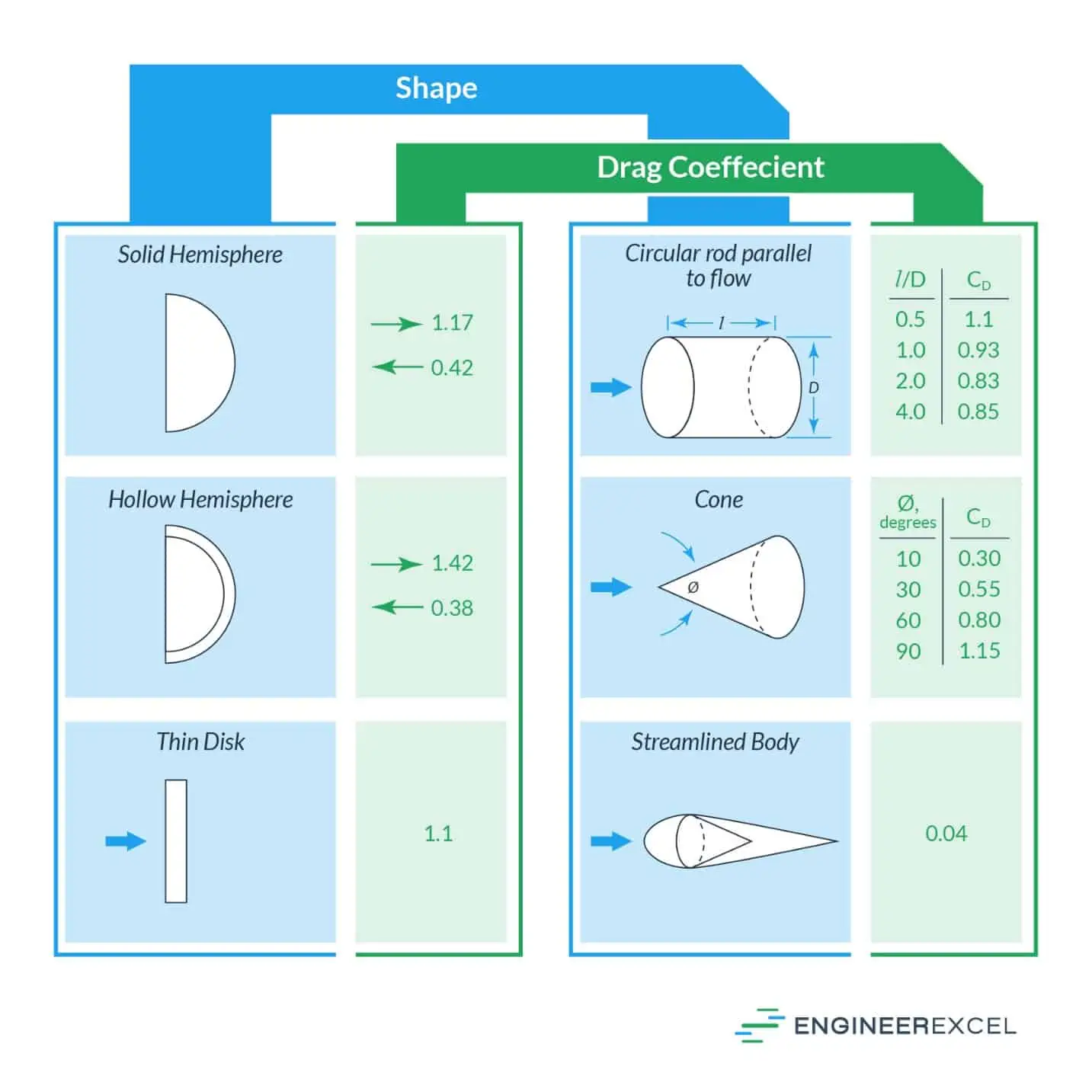
Different bodies will have different aerodynamic properties that affect the drag imparted. The drag coefficient, CD, describes how much a body’s shape affects its drag. A higher drag coefficient indicates that the shape is less aerodynamic, and will have a higher induced drag force under the same conditions. For example, a streamlined body is more aerodynamic than a thin disk:

Elevate Your Engineering With Excel
Advance in Excel with engineering-focused training that equips you with the skills to streamline projects and accelerate your career.
In addition to the drag coefficient, there are other parameters specific to a given scenario that must be considered when calculating the induced drag. Ultimately, the drag equation combines these parameters to provide a calculated value for the induced drag.
Drag Equation Parameters
The drag induced on an object as it moves through the air (such as an aircraft or rocket) is constrained by several parameters. These parameters are introduced below.
Air Density
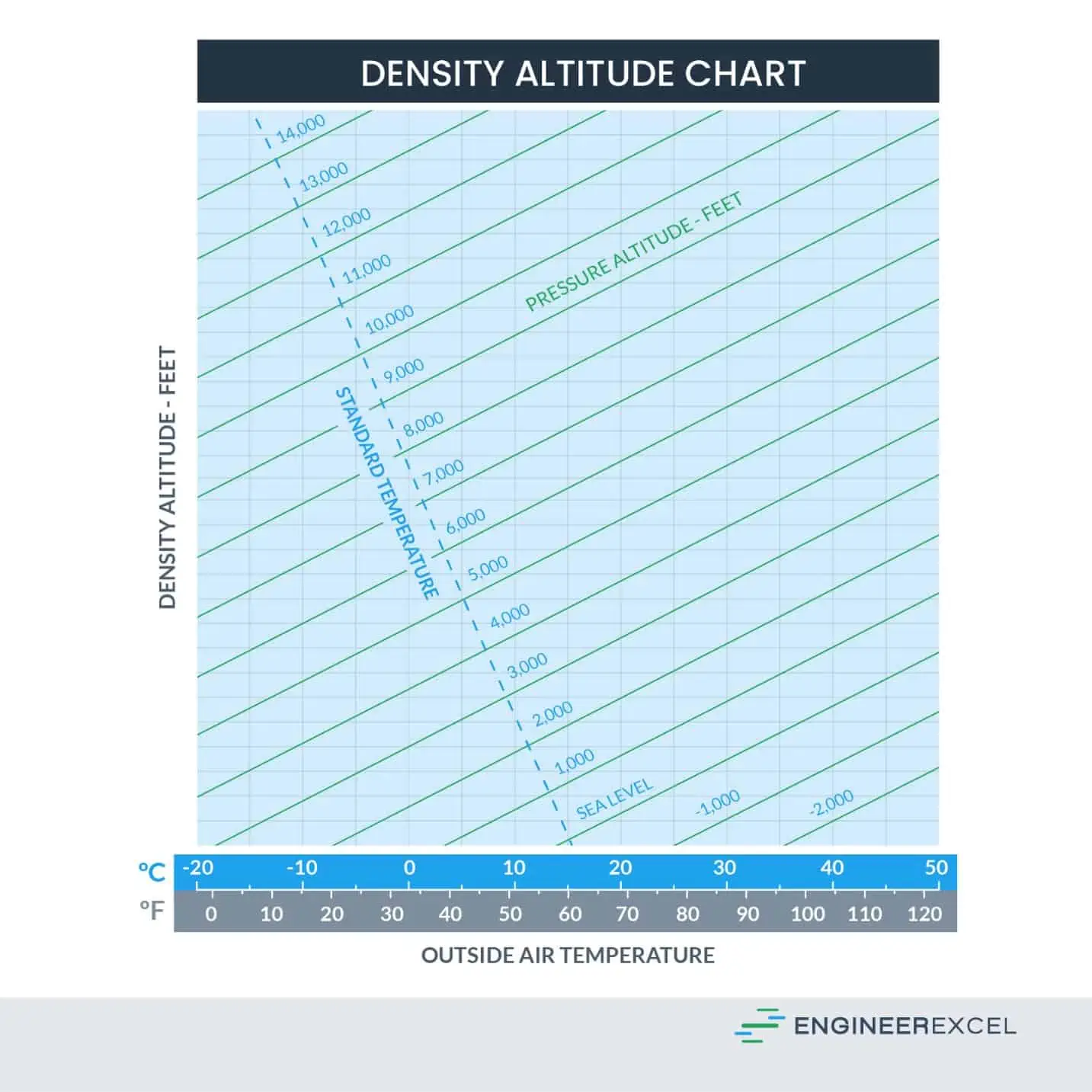
The density of the air through which an object moves plays an important role in the drag induced on the object. In general, air density decreases with altitude. To determine the air density, a look-up table is often used in preliminary engineering calculations. An example of such a look-up table is shown below:
Velocity
Another key drag calculation parameter is the velocity of the object. An object moving faster will be subject to increased drag, with the drag increasing in relation to the velocity squared.
Area
The area of the object also plays a role in the drag induced on the object. Specifically, it is the reference area, which is the area exposed to the air flow. This is contingent on the size and shape of the object, as well as the angle of the object as it moves.
Additional Air Properties
There are other properties of the air, including its viscosity and compressibility, that also affect the induced drag. These air properties are extremely variable and interact with each other. To include these factors into the calculation of drag, a drag coefficient is applied.
Drag Coefficient
The drag coefficient of an object is something that has been previously calculated through experimentation. This coefficient embodies several properties and parameters into a single dimensionless value, greatly simplifying the calculation of the drag.
The way in which area is defined will affect the value of the drag coefficient.
Drag Equation
Using the parameters for a given situation, the drag induced on a body moving through the air is calculated using the following equation:

where:
- CD is the drag coefficient, which is a dimensionless value
- ρ is the density of the air, with units of lb/ft3
- v is the velocity of the body, with units of ft/s
- A is the reference area of body, with units of ft2
From the above equation, the relationship among the various parameters can be seen, and how they apply to the calculation of the drag induced on an object moving through air.

Since the density of the air decreases with altitude, a plane flying at a higher altitude will experience less drag. This is why commercial aircraft usually fly at around 30,000 ft, where the air density is approximately 0.02272 lb/ft3, compared to the density at sea level, which is 0.0765 lb/ft3.
As the drag is related to the square of the velocity, an object’s velocity has the largest impact on the induced drag. Again, using an airplane as an example, flying at a speed of 500 mph (about 730 ft/s) vs flying at a speed of 200 mph (about 290 ft/s) will have more than six times the drag.
The reference area of the body takes into consideration the area perpendicular to the flow. The reference area of an object will change with the object’s orientation. This plays a key role in the aerodynamics of an object. An airplane will fly through the air in such a way as to minimize its reference area.
Overcoming Drag
When flying, an aircraft or rocket will need to overcome the aerodynamic drag the air induces upon it. Because the velocity of the body plays such a large role in the calculation of the drag force, it is important to consider how something moving faster will require additional force to overcome the additional drag.
For an aircraft, the jet engines or propeller imparts a thrust that counteracts the induced drag. For stable flight, i.e., constant velocity, the balance of forces means the thrust will be equal to the induced drag force. To enable the aircraft to accelerate, the engines must produce more thrust than the induced drag, however, as the aircraft accelerates, the velocity will increase, increasing the drag.
For a rocket, whose shape has been honed to present the most aerodynamic shape to minimize drag, the rocket engines produce must produce a very large amount of thrust to power the rocket through the lower atmosphere, where the lower velocity counteracts the higher atmospheric density. As the rocket gains altitude, the atmospheric density decreases, and the velocity increases with decreasing induced drag and reduced rocket mass.
Example Calculation
Taking an airplane in a scenario with the following parameters, the drag can be calculated.
- Flying at 36,000 ft, where the density of the air is 0.02285 lb/ft3
- Reference area of 220 ft2
- Flying at a velocity of 600 mph = 880 ft/s
In this example, the drag coefficient has been predetermined using modeling analysis to be 0.024. Using the above parameters, the drag is calculated as follows:

In this scenario, the aircraft’s engines will need to produce 1.5×106 lbf of thrust to overcome the induced drag and maintain steady flight. To accelerate, the engines will need to produce additional thrust, which will, in turn, increase the velocity and the induced drag.
Additional Applications
In addition to calculating the drag to be able to understand the thrust required for an object, the drag can also be used in its relationship with the lift of a body. Specifically, the lift-to-drag ratio is a parameter that can be used when optimizing an aerodynamic engineering design.
Fluid Dynamics
Although most often applied in aerodynamics, the drag equation is generally applicable in fluid dynamics, i.e., the movement of a fluid, which includes both liquids and gases. For example, the drag equation remains the same when calculating induced drag on a submarine in the ocean. In this case, the density parameter will be for the water and the drag coefficient will be changed to consider the different scenario, but the overall calculation remains the same.
Terminal Velocity
A key concept when considering the calculation of aerodynamic drag is the terminal velocity. This is the velocity at which the drag is maximum and completely counteracts any external acceleration. The terminal velocity is usually applied to objects falling through the air, and will specify the velocity that an object will reach before the induced drag force is exactly equal to the force due to gravity.
