When a solid body moves relative to the viscous fluid surrounding it, a net force is exerted on the body. The magnitude of this force is influenced by various factors, including the relative velocity, the shape and size of the body, and the properties of the fluid.
This article specifically examines the drag coefficient, which is a fundamental unitless parameter used to describe the resistance encountered by an object as it moves through the fluid medium.
Drag Coefficient Units
The drag coefficient is a unitless quantity that represents the magnitude of resistance experienced by an object moving through a fluid medium. It is a fundamental parameter used to characterize the aerodynamic or hydrodynamic behavior of the object.
Drag Force
Before learning about drag coefficient in detail, it is important to understand the concept of drag force.

Elevate Your Engineering With Excel
Advance in Excel with engineering-focused training that equips you with the skills to streamline projects and accelerate your career.
Drag force refers to the collective pressure and frictional force that opposes the motion of an object as it moves through a fluid medium, such as air or water. Hence, it is also referred to as fluid resistance or air resistance.
Consider a moving airplane shown below.

As an airplane travels through the air, the molecules of air interact with the surface of the plane, generating frictional forces that oppose the direction of the plane’s motion. These combined frictional forces give rise to an airplane’s drag force.
The magnitude of the drag force is influenced by various factors, such as the object’s shape and size, the relative speed between the object and the fluid, the density of the fluid, and the viscosity of the fluid. In general, larger objects or those with intricate shapes encounter higher drag forces in comparison to smaller and streamlined objects.
The drag force can be written in functional form as:
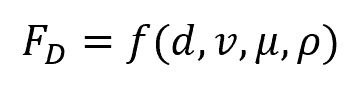
Where:
- FD = drag force [N]
- d = diameter or characteristic length [m]
- v = fluid velocity [m/s]
- μ = fluid viscosity [Pa-s]
- ρ = fluid density [kg/m3]
From Bernoulli’s equation, the value of the drag force for incompressible fluids can be calculated using the formula:
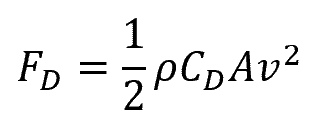
Where:
- A = reference area [m2]
- CD = drag coefficient [unitless]
The drag force plays a crucial role in a wide range of applications, including aerodynamics, automotive engineering, and fluid dynamics. When designing vehicles, structures, or any objects that interact with fluids, it is vital to take into account the effect of drag force as it can affect the performance, stability, and efficiency of such systems.
Drag Coefficient
Analyzing the behavior of fluids can be complex due to the numerous dependencies at play. To simplify these complex relationships, one approach is to summarize the dependencies using a single variable. In the case of drag force, this variable is known as the drag coefficient.

The drag coefficient is a dimensionless parameter that relates the drag force on an object to its size, shape, and velocity relative to the fluid. It is also influenced by the surface properties and flow conditions of the fluid. In general, it provides a concise characterization of how these diverse factors collectively impact drag, making the analysis of fluid dynamics more manageable.
A lower drag coefficient signifies that the object has a streamlined shape and encounters less resistance from the fluid, resulting in reduced drag. On the other hand, a higher drag coefficient suggests that the object experiences greater resistance when moving through the fluid.
Rearranging the above equation for drag force, the formula for drag coefficient can be written as:
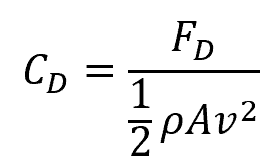
Note that the term ½ρv2 is equal to the dynamic pressure. Hence, the drag coefficient can also be mathematically expressed as:

Where:
- q = dynamic pressure [Pa]
In general, if compressibility and free-surface effects are considered, then drag coefficient can be written in functional form as:
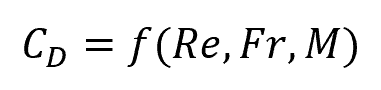
Where:
- Re = Reynolds number [unitless]
- Fr = Froude number [unitless]
- M = Mach number [unitless]
The Reynolds number is a measure of how inertial forces compare to viscous forces in fluid flow. It helps identify the type of flow regime—either laminar or turbulent. The drag coefficient can change with the Reynolds number as the flow regime transitions.
The Froude number relates fluid flow inertia to gravitational forces. It characterizes flow behavior concerning surface waves, particularly in the context of open-channel flows.
The Mach number indicates the ratio of fluid flow velocity to the local speed of sound. It is commonly used to assess compressibility effects in high-speed flows. Changes in the Mach number can significantly impact the drag coefficient, especially during transitions from incompressible to compressible or from subsonic to supersonic regimes.
These parameters can collectively affect the resistance experienced by an object in a fluid flow, depending on the flow conditions and object properties.
Measurement of Drag Coefficient
The drag coefficient is a crucial parameter in aerodynamics and hydrodynamics, as it helps engineers understand and predict the behavior and movement of objects through fluid, such as airplanes, cars, ships, and even sports equipment. By comparing the drag coefficient of different objects or configurations, engineers and scientists can assess and optimize their designs for improved performance, reduced energy consumption, or enhanced efficiency.
Finding the value of the drag coefficient can be difficult since it may involve multiple sources of drag, such as form, skin friction, and wave components. Hence, instead of mathematically computing for the coefficient, its value is almost always determined experimentally using computational fluid dynamics simulations. In the case of air, this is done using a wind tunnel, as shown below.
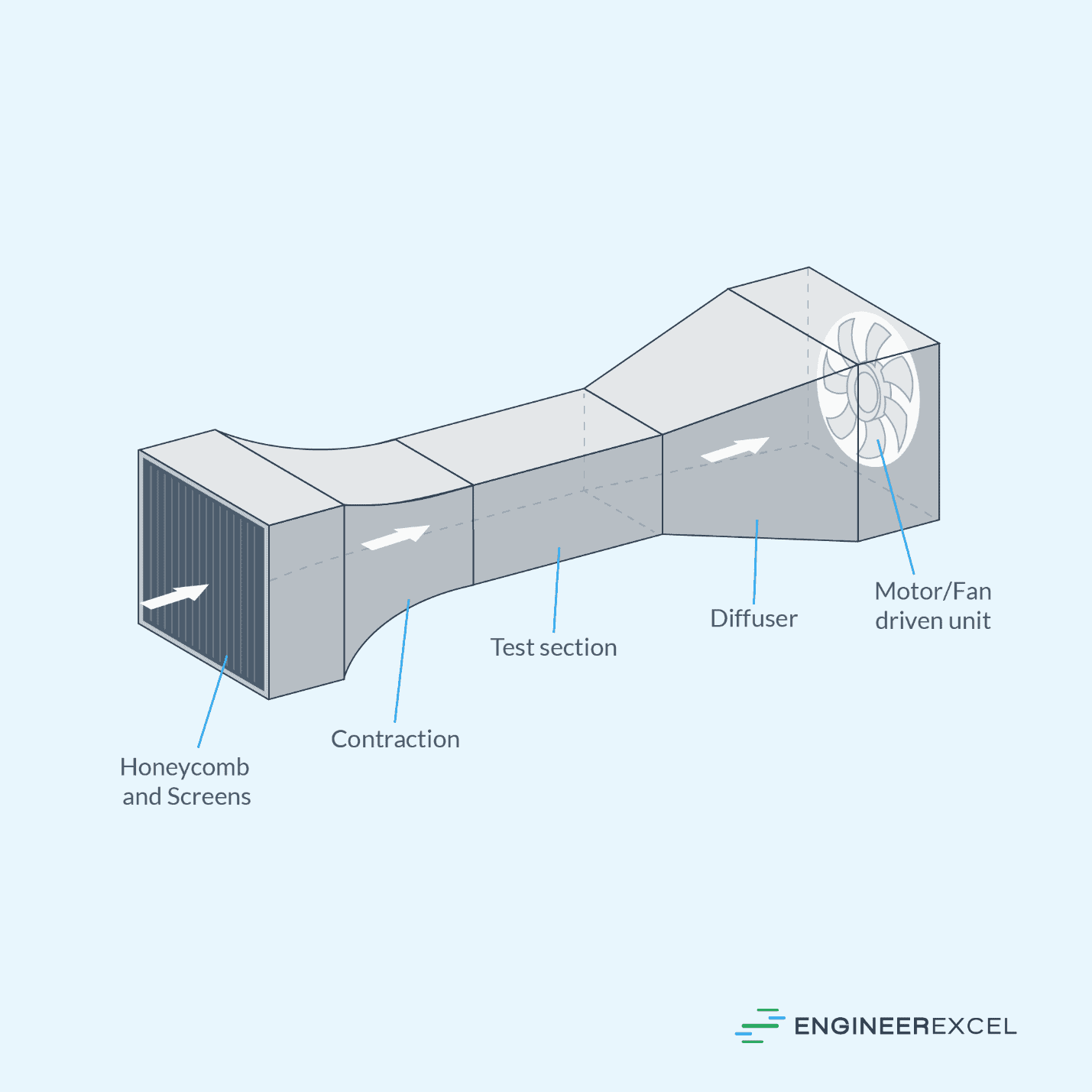
A wind tunnel is a specialized facility used for studying the aerodynamic properties of objects by subjecting them to controlled airflow. The drag coefficient is usually determined by selecting a reference area and measuring the drag force, and then using the formula above to calculate the coefficient. This value normally depends on parameters, such as the body shape, Reynolds number, and surface roughness.
Note that the choice of reference area depends on application and operating conditions. For example, if majority of the drag force is being caused by friction between the air and the body, a logical choice for the reference area would be the total surface area of the body. On the other hand, if the drag force is caused by the resistance to the flow, a more logical choice would be the frontal area of the body that is perpendicular to the flow direction.
If the goal is to compare the drag coefficient with the lift coefficient, the same wing area used to derive the lift coefficient should be used. In aerodynamics, the reference area for airplanes is often the wing area.
In automotive engineering, it may be the frontal area of a vehicle. In naval architecture, it may be the wetted area of a ship or barges.
In practical applications, drag coefficients are commonly reported for various areas of the same object. In the report, the test engineer needs to specify the specific area used for the measurements. When utilizing the data, the reader might need to convert the drag coefficient using the ratio of their desired area to the specified area.
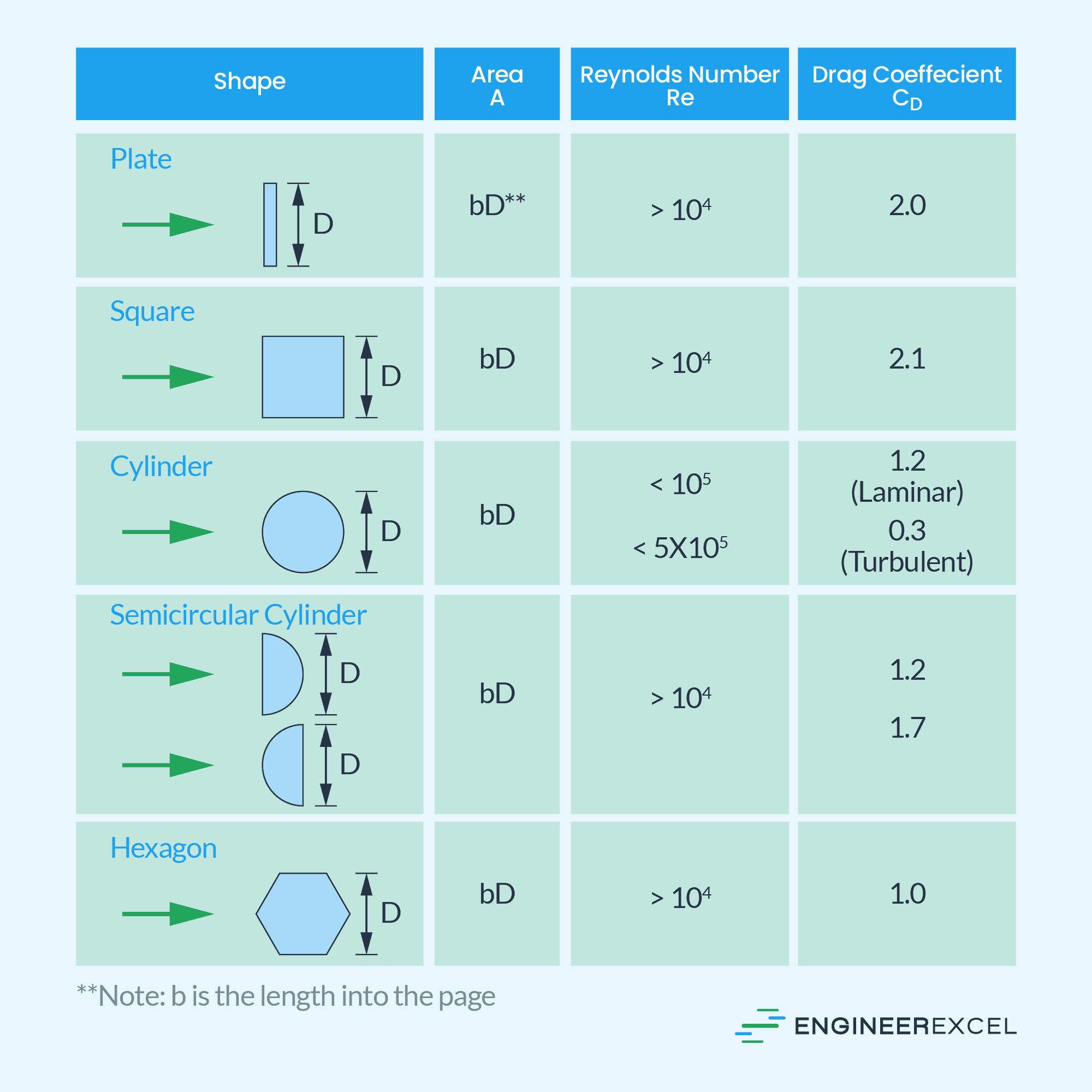
Drag Coefficient Values
Given the area and Reynolds number, here are some of the estimated values of drag coefficients for flow over simple two-dimensional and three-dimensional bodies, summarized in the following tables.