In engineering, a fundamental concept is the conservation of mass, which states that the mass of a system, whether that system is static or dynamic, will always remain constant. This can be explained using the following equation:
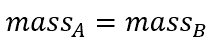
Some practical engineering examples of the conservation of mass include solid mechanics, fluid statics, and fluid dynamics.

Conservation Of Mass Equation For Solid Mechanics
In solid mechanics, which addresses how solid structures move and react to forces, the conservation of mass specifies that the mass within the system remains constant. In other words, mass is not created or destroyed within the system. In any application of solid mechanics to engineering, such as the deformation of a beam, the mass of an object, which has SI units of is calculated as follows:

Elevate Your Engineering With Excel
Advance in Excel with engineering-focused training that equips you with the skills to streamline projects and accelerate your career.
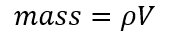
where:
- ρ is the density of the material, with SI units of kg/m3
- V is the volume of the object, with SI units of m3
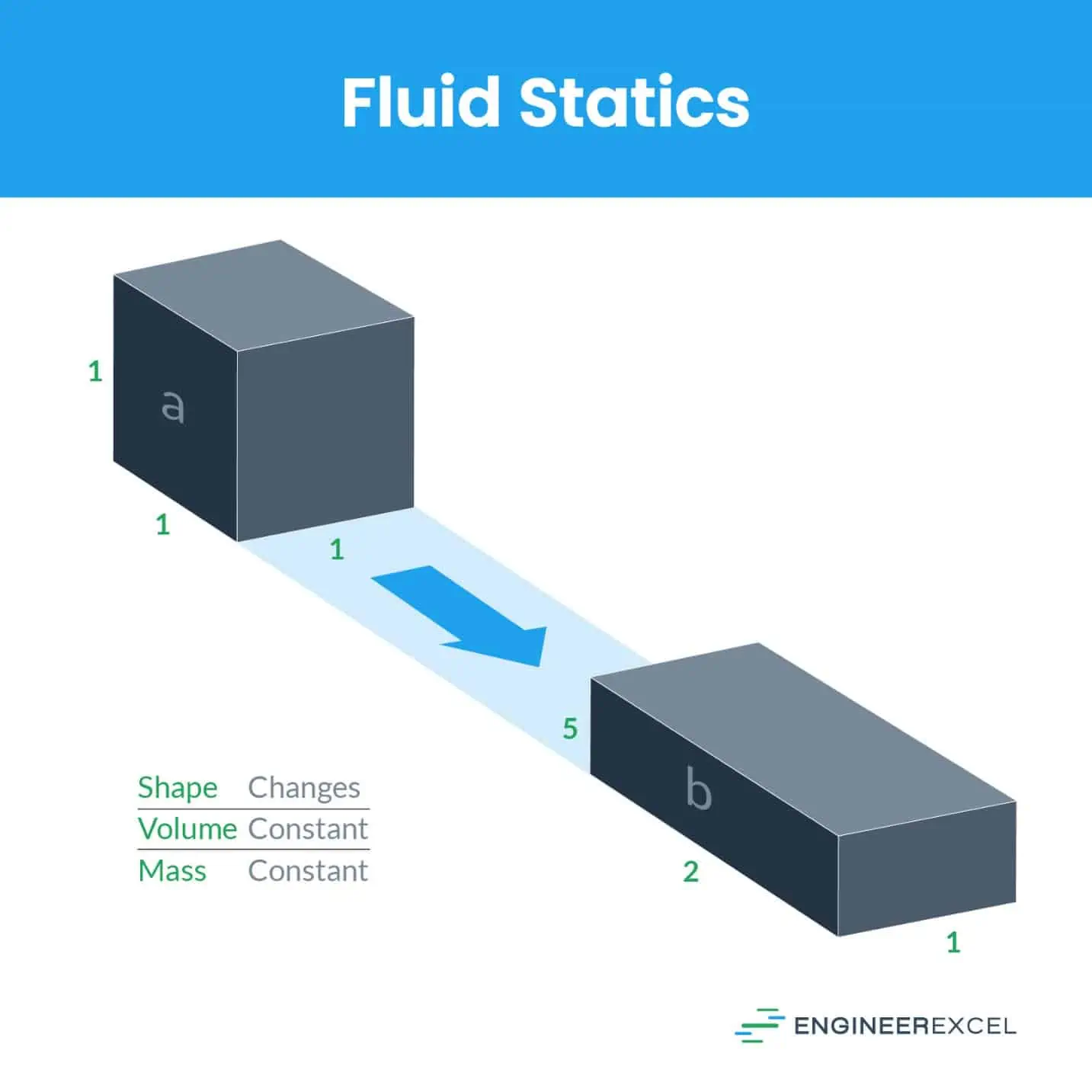
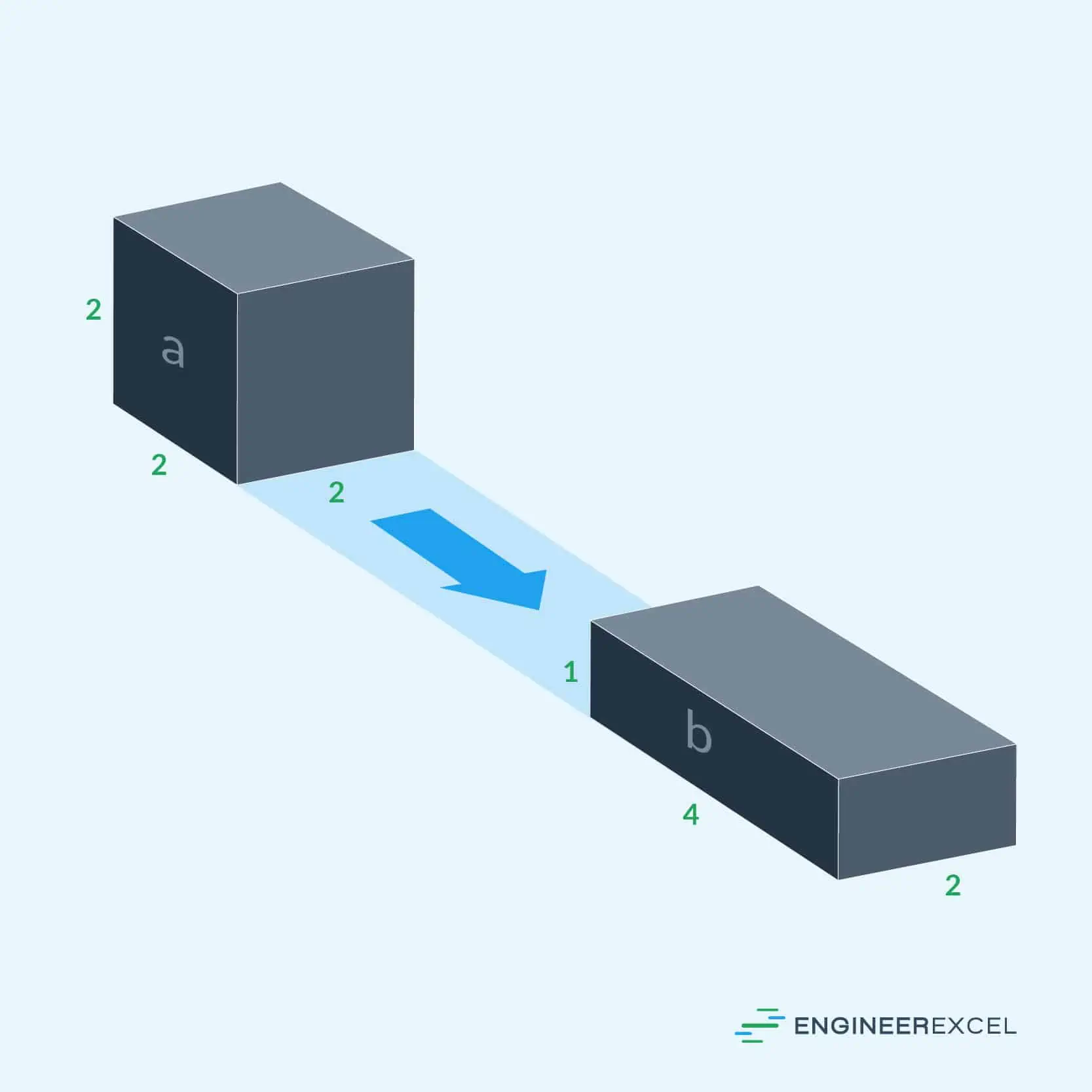
Under a static transformation, the object shape remains constant, the object volume remains constant, and, therefore, the mass remains constant. The following image demonstrates this concept:
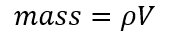
In the above image, the mass of the object, a, is translated to b without any change in shape or volume, which means that the mass of b is the same as that of a.
Example Calculation
An example of the conservation of mass in solid mechanics explores a situation of a beam made of AISI 4037 steel, which has a density of 7850 kg/m3. The cross-section of the beam is as follows:

This beam is translated 10 m along its x-axis from A to B with no change in its shape or volume as follows:

To demonstrate the conservation of mass, the following steps are taken:
- Calculate the initial volume at A:
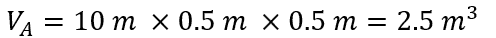
- Calculate the initial mass at A:
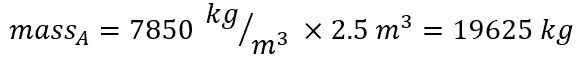
- Because there is no change in shape or volume as the beam is shifted from A to B,
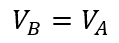
Therefore,
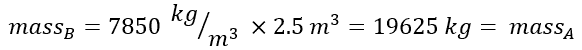
Conservation Of Mass Equation For Fluid Statics
In fluid statics, which addresses a fluid (gas or liquid) that remains in the same place, the volume of the fluid remains constant but its shape may change within the system. One of the fundamental properties of a fluid is that its shape will change to fill the volume in which it is contained. The following image shows an example of a change in shape with constant volume:
In the above image, the volume of the container in a is the same as in b, but the shapes of the two states are clearly different. Using the mass calculation equation, because the volume remains the same between the two states, the mass will remain the same.
Example Calculation
An example of the conservation of mass in fluid statics explores a situation of a container filled with liquid oxygen, which has a density of 1140 kg/m3. The container’s shape changes as follows:
To demonstrate the conservation of mass, the following steps are taken:
- Calculate the initial volume at A:
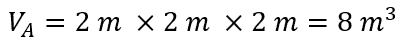
- Calculate the initial mass at A:
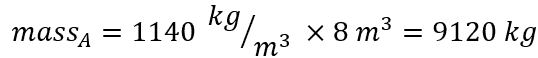
- Calculate the final volume at B:
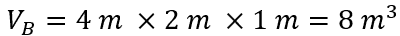
- Calculate the final mass at B:
Conservation Of Mass Equation For Fluid Dynamics
In fluid dynamics, which addresses a fluid moving through a system, the area of the system may change but the volume remains the same, similar to a scenario in fluid statics. Again, as the fluid moves through the system, which may be a pipe or duct, the cross-sectional area of the pipe could increase or decrease, but the volume remains the same.
In fluid dynamics, the mass of the fluid flowing through a specific cross-section can be calculated using the following equation:
where:
- t is the time during which the fluid moves, with SI units of s
- v is the velocity with which the fluid moves, with SI units of m/s
- A is the cross-sectional area of the system, with SI units of m2
Example Calculation
As an example of the conservation of mass of a fluid moving through a system, consider liquid oxygen moving through a pipe whose cross-sectional area changes from to . In fluid mechanics, as the cross-sectional area of a pipe changes, the velocity of the fluid will change in inverse proportion. The change in velocity can be calculated as follows:

The initial velocity of the liquid oxygen is 10 m/s.
To demonstrate the conservation of mass, the following steps are taken:
- Calculate the velocity at B:
- Calculate the mass moving through A over a period of :
- Calculate the mass moving through B over the same period of :
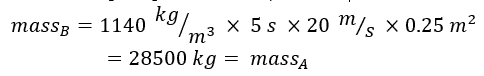
The conservation of mass is a fundamental physical limitation, which can be simplified to state that mass cannot be created or destroyed. In the above examples in solid mechanics, fluid statics, and fluid dynamics, practical engineering solutions demonstrate that mass remains the same throughout the system.
For reference, in situations involving things like black holes or exotic systems, the conservation of mass no longer applies. However, these scenarios are currently beyond the scope of practical engineering analysis.
